We are faced with compelling observational evidence that the universe contains more matter than antimatter. Unless we are willing to make the unappealing assumption that the initial condition of the universe was matter-antimatter-asymmetric, we have to find a mechanism to generate the asymmetry from symmetric initial conditions. This process of generating the asymmetry is called ``baryogenesis''. It was Sakharov who first proposed that the universe might have started out symmetric, and who determined the conditions that any baryogenesis mechanism must fulfill [6]. These conditions are called the ``Sakharov conditions'' in his honor. We summarize them in the following section; then we discuss the various asymmetry generation mechanisms that have been proposed.
To produce a matter-antimatter asymmetry from equal initial abundances of matter and antimatter, the baryogenetic mechanism must satisfy the following conditions:
The Standard Model of particle physics contains all the ingredients
necessary to satisfy the Sakharov conditions.
![]() violation is
described by the Kobayashi-Maskawa mechanism [7].
violation is
described by the Kobayashi-Maskawa mechanism [7].
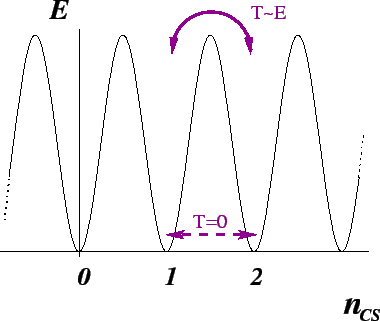
![]() violation is implemented in ``sphaleron'' interactions. These
interactions are in some ways like quantum tunneling. The vacuum has
a degenerate ground state, but the ground states are separated by an
energy barrier. (See the sketch in Fig. 5.) In making the
transition from one ground state to the other,
violation is implemented in ``sphaleron'' interactions. These
interactions are in some ways like quantum tunneling. The vacuum has
a degenerate ground state, but the ground states are separated by an
energy barrier. (See the sketch in Fig. 5.) In making the
transition from one ground state to the other, ![]() and the lepton number
and the lepton number
![]() are violated. At low temperature these transitions are rare because
of the height of the barrier; at higher temperature they can occur much
more frequently and lead to large
are violated. At low temperature these transitions are rare because
of the height of the barrier; at higher temperature they can occur much
more frequently and lead to large ![]() and
and ![]() violation. The sphaleron
mechanism violates
violation. The sphaleron
mechanism violates ![]() and
and ![]() but conserves
but conserves ![]() ; this will be
important in a few sections when we discuss leptogenesis.
Finally, a departure from equilibrium may occur when the electroweak
symmetry is broken; whether this is the case depends on the mass of
Higgs boson.
; this will be
important in a few sections when we discuss leptogenesis.
Finally, a departure from equilibrium may occur when the electroweak
symmetry is broken; whether this is the case depends on the mass of
Higgs boson.
The current limit on the Higgs mass (![]() GeV) almost
rules out the electroweak phase transition as a source of
disequilibrium. The large mass of the Higgs combined with the smallness
of the observed
GeV) almost
rules out the electroweak phase transition as a source of
disequilibrium. The large mass of the Higgs combined with the smallness
of the observed ![]() violation almost entirely excludes the parameter
space in which the standard model can account
for the observed baryon asymmetry. Supersymmetric extensions to the
standard model expand the parameter space; we will know a great deal
more about the feasibility of electroweak baryogenesis once
supersymmetry is explored experimentally at the next generation of
colliders.
violation almost entirely excludes the parameter
space in which the standard model can account
for the observed baryon asymmetry. Supersymmetric extensions to the
standard model expand the parameter space; we will know a great deal
more about the feasibility of electroweak baryogenesis once
supersymmetry is explored experimentally at the next generation of
colliders.
 |
At the Planck scale we expect quantum gravity to become the dominant interaction. In quantum-gravitational interactions, we should not expect any quantum numbers to be conserved. An intuitive way to see this is to note that black holes are fully described by their mass, their angular momentum and their entropy; quantum-gravitational interactions involving the exchange of virtual black holes therefore have no knowledge of the interacting particles' other quantum numbers and can violate all of them.
If quantum gravity is the mechanism for baryogenesis, then we are in an
unfortunate position; the relevant energy scale is ![]() GeV, which
will remain inaccessible to colliders for the foreseeable future. We'll
be left with a mechanism untestable by experiment. We can draw comfort
from the following argument. The Planck scale is in all likelihood
higher than the energy scale at the end of inflation; whatever baryon
excess was generated by quantum gravity is washed out by inflation; and
so the present-day baryon excess is probably not generated by quantum
gravity. That clears the way for a more testable mechanism.
GeV, which
will remain inaccessible to colliders for the foreseeable future. We'll
be left with a mechanism untestable by experiment. We can draw comfort
from the following argument. The Planck scale is in all likelihood
higher than the energy scale at the end of inflation; whatever baryon
excess was generated by quantum gravity is washed out by inflation; and
so the present-day baryon excess is probably not generated by quantum
gravity. That clears the way for a more testable mechanism.
The strong, weak and electromagnetic couplings, when extrapolated from the
energies that are currently experimentally accessible to us, are
approximately equal to each other at
![]() GeV. This
observation has motivated theorists to propose that the strong and
electroweak interactions ``unify'' at that energy. Theories that
accomplish this unification are called ``grand unified theories''
(GUT).
GeV. This
observation has motivated theorists to propose that the strong and
electroweak interactions ``unify'' at that energy. Theories that
accomplish this unification are called ``grand unified theories''
(GUT).
These theories involve heavy bosons (
![]() GeV) that couple
quarks to leptons.
GeV) that couple
quarks to leptons. ![]() violation is in effect built into GUTs from the
start.
violation is in effect built into GUTs from the
start. ![]() violation can come from KM mechanism as in the standard
model or from the newly introduced couplings to the heavy bosons. Thus,
it is possible that baryogenesis occurred at the GUT energy scale.
violation can come from KM mechanism as in the standard
model or from the newly introduced couplings to the heavy bosons. Thus,
it is possible that baryogenesis occurred at the GUT energy scale.
GUT-scale baryogenesis poses a similar problem to Planck-scale
baryogenesis. It occurs at energies so high that it eludes testing
in terrestrial experiments. Once again we can take heart in the fact
that inflationary scenarios disfavor this mechanism. If the reheating
of the universe at the end of inflation exceeds a certain temperature,
more WIMPs are produced than is consistent with the observed ![]() .
In many circles the reheating temperature limit is believed to lie below
the GUT scale, ruling out GUT baryogenesis after the inflationary era.
.
In many circles the reheating temperature limit is believed to lie below
the GUT scale, ruling out GUT baryogenesis after the inflationary era.
Leptogenesis [8] is currently the favored mechanism for
baryogenesis. In this
mechanism the universe first acquires a lepton excess, which is then
converted into a baryon excess by a process that violates ![]() and
and ![]() but conserves
but conserves ![]() -- for example the standard-model sphaleron
mechanism.
-- for example the standard-model sphaleron
mechanism.
The initial lepton excess that is required in this mechanism can come from,
for example, heavy Majorana neutrinos (![]() ). A Majorana neutrino is its
own antiparticle. If the Majorana neutrino decays, for example, to a
Higgs boson and a light lepton,
). A Majorana neutrino is its
own antiparticle. If the Majorana neutrino decays, for example, to a
Higgs boson and a light lepton,
![]() , then the
, then the ![]() -conjugate decay is
-conjugate decay is
![]() . If
. If ![]() is violated, then the decay
rates of the
is violated, then the decay
rates of the ![]() into
into ![]() and
and
![]() can differ, and the
universe can end up containing more leptons than antileptons:
can differ, and the
universe can end up containing more leptons than antileptons:
The reason the leptogenesis mechanism is popular is that the parameter
space in which it is viable has not yet been constrained almost to
death, as is the case for standard-model electroweak baryogenesis. At
the same time, a major test of its viability is not too far in the
future: within the decade, experiments should tell us the magnitude
of ![]() violation in the neutrino sector.
violation in the neutrino sector.
The Affleck-Dine scenario for baryogenesis notes that in supersymmetric
theories, where each of the ordinary fermion fields from standard-model
physics has a scalar partner, the early universe contained baryon- and
lepton-number-carrying scalar fields. Through interactions with the
inflaton field ![]() -violating and
-violating and ![]() -violating effects can be
introduced. As the scalar particles decay to fermions, the net baryon
number the scalars carry can be converted into an ordinary baryon
excess [9]. ([9] is a recent and very
thorough review not only of Affleck-Dine baryogenesis but of
baryogenesis in general.)
-violating effects can be
introduced. As the scalar particles decay to fermions, the net baryon
number the scalars carry can be converted into an ordinary baryon
excess [9]. ([9] is a recent and very
thorough review not only of Affleck-Dine baryogenesis but of
baryogenesis in general.)
The Affleck-Dine mechanism is also a mechanism for dark-matter creation.
Fluctuations in the scalar quark fields (``Q-balls'') are a dark-matter
candidate if they are stable. If they are unstable, they can still
decay into dark matter. If the Affleck-Dine mechanism is indeed played
out in nature, then its dual role of producing baryons and producing
dark matter opens up the possibility of explaining the ratio between
![]() and
and
![]() from first principles.
from first principles.